为了从有理数推导出实数结构，我们知道有理数在实数中是密集的，意思是在任意两个实数之间存在一个有理数。这个简单的观察引出了一个关键的事实：每一个实数都是有理数序列的极限。因此，有理数的收敛序列使我们能够得到所有的实数。由于许多不同的有理数数列都可能收敛于同一实数。我们需要在它上面引入一个等价关系，它识别两个有理数序列，如果它们收敛于相同的实数。

综上所述，如果S表示所有的有理数序列收敛的集合，那么我们期望能够确定一个等价关系~ S，使S/ ~形成实数的模型。然而，为了在不进入循环论证的情况下迈出第一步，我们必须首先能够在没有任何实数先验知识的情况下识别出所有有理数序列中的收敛序列。这是通过引用柯西数列的概念来完成的，柯西数列是实数数列的一个条件，众所周知，它等价于收敛。关键的观察是，有理数序列的柯西条件可以完全不提及实数。

超越数

在数学中，超越数是非代数数，也就是说，不是一个有限次有理数多项式的根。最著名的超越数是π和e。

虽然只有少数几类超越数是已知的，超越数并不罕见。事实上，几乎所有的实数和复数都是超越的，因为代数数构成了可数集，而实数集和复数集都是不可数集，因此大于任何可数集。所有超越的实数（也称为实数超越的无理数或超越的无理数）都是无理数，因为所有有理数都是代数数，但并不是所有的无理数都是超越的。因此，实数集由有理数、代数无理数和超越实数组成。例如，2的平方根是无理数，但它不是超越数。黄金比例是另一个非超越数的无理性数。

约瑟夫·刘维尔直到1844年才确立了超越数的存在，不久之后，他构建了第一个明确的超越数的例子。虽然我们对超越数已经了解了很多，但π +e是否是代数的还是未知的。

1884年，继刘维尔证明了超越数的存在之后不久，康托不仅证明了超越数的存在，而且还证明了绝大多数实数在某种意义上是超越的。康托使用的技术是超限计数法。利用集合的基数概念，康托计算了有多少个代数数和有多少个实数，并证明了实数严格地多于代数数。超越数存在这一不可避免的结论，虽然遇到了一些阻力，却迫使我们面对下面同样不可避免的真理。与康托的代数数计算类似，我们也可以计算任何自然语言中的所有句子，例如英语。正如它所证明的，所有潜在的英文实数描述的基数与代数数的基数是相同的，因此严格小于所有实数的基数。我们现在必须得出这样的结论：存在一些实数，它们永远不可能被描述为任何形式。

线性空间

线性空间，也被称为向量空间，可能是数学空间中最简单的概念。当被认为是模拟实际的物理空间时，线性空间似乎在所有方向上都是相同的，并且完全没有任何曲率。线性空间，以及与线性变换或线性算子密切相关的概念，是基本的对象。例如，函数在一点上的导数最好理解为切线空间上的线性算子，特别是对于多变量函数。可微流形是非常复杂的空间，但在每一点上，它们都是局部线性的。这可能有点夸张，但众所周知，如果一个问题可以线性化，那么它就等于解决了。

拓扑空间

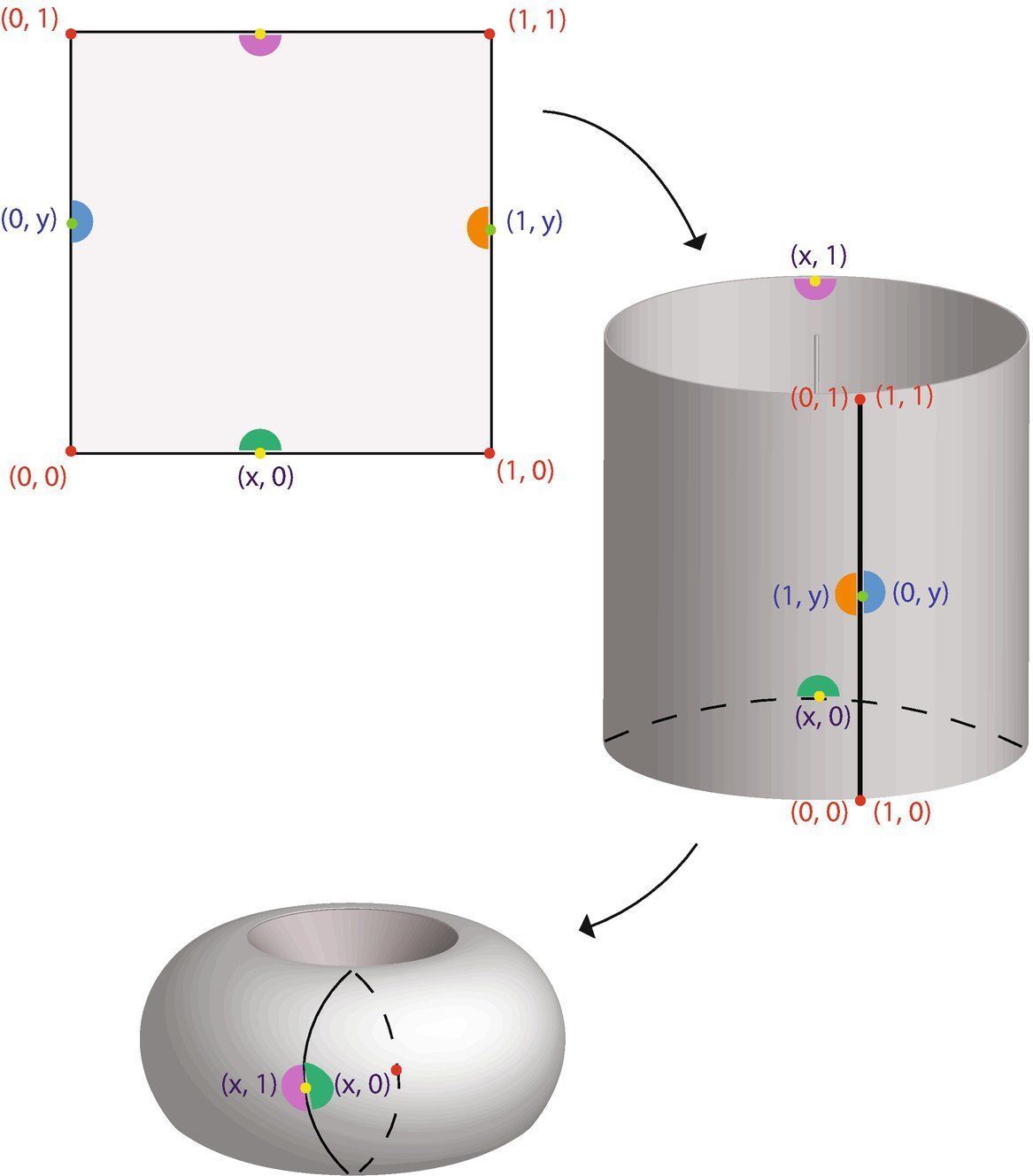
拓扑很容易定义，但很难解释。导致拓扑学发展的思想在表面之下潜伏了一段时间，很难确定拓扑学在历史上的确切时间诞生。可以肯定的是，拓扑学诞生后，在20世纪上半叶的发展非常迅速。拓扑的统一能力是巨大的，它的解释能力是强大的。例如，连续函数在闭区间上的极大极小的存在性，或连续函数在闭区间上的一致连续性，可能使闭区间显得具有特殊意义。拓扑学能够解释这种情况，确定闭区间的一个特定拓扑性质，即它是紧凑的，作为使证明能够延续到更一般情况下的关键成分。

度量空间（距离空间）

度量空间出现在1906年莫里斯的博士论文t中。度量空间是可以测量点之间距离的集合，从某种意义上说，度量空间所携带的几何信息比拓扑空间所能描述的要多得多。公理越强，定理越强，但例子也越少。然而，度量空间的公理允许大量和各种各样的例子和定理。特别地，完全度量空间，即那些直观上没有孔的度量空间，有两个很强的定理。一个是巴拿赫不动点定理，另一个是贝瑞定理（Baire's Theorem）。前者可用于求解微分方程，而后者对完备度量空间和连续函数的结构有深刻的影响。

文章来源：《应用数学和力学》 网址: http://www.yysxhlx.cn/zonghexinwen/2022/0422/1312.html

上一篇：北大数学天才柳智宇，毕业后却出家当和尚，大
下一篇：薛定谔方程，从数学上看经典力学是如何产生量